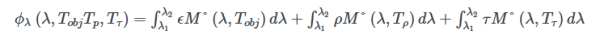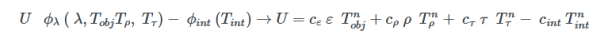기술 자료실

온도 계산 (Temperature Calculation)

적외선 복사의 전기 신호 변환과 물체 온도 계산

적외선 센서는 물체 표면에서 방출되는 적외선 복사, 즉 복사 플럭스(radiative flux)를 측정하여 물체의 온도를 결정합니다. 방사 에너지는 물체의 온도와 재료별 방사율(emissivity)의 함수입니다. 또한, 열 센서는 도달하는 다른 적외선 플럭스도 감지합니다. 여기에는 반사된 주변 복사, 내부 복사, 투과 복사가 포함됩니다. 측정된 복사를 온도 값으로 변환하기 위해, 적외선 센서는 Planck의 법칙에 기반한 보정 모델을 사용하고, 목표 물체 재료의 알려진 또는 추정된 방사율을 포함하며, 더 복잡한 경우 광학적 환경에 대한 정보도 포함합니다.

가장 단순한 경우, 하나의 방사원과 협대역 파장만 고려하면, Planck의 법칙은 회색체(gray body)의 스펙트럼 복사 방출 Mλ∘(λ,T)를 온도 T와 파장 λ, 방사율 ε의 함수로 정의하며, c₁과 c₂는 Planck의 첫 번째와 두 번째 상수입니다.

이 방정식을 역으로 풀면 주어진 스펙트럼 복사에 대한 온도를 구할 수 있으며, 방사율을 포함합니다.

그림 1. 물체는 온도에 따라 적외선을 방출하며, 주변 복사의 일부를 반사합니다.

투명 물체는 다른 적외선 복사도 통과시킵니다. 센서는 합성된 복사 플럭스를 감지하며,

물체의 실제 온도를 정확히 결정하기 위해 주변 반사와 내부 복사 보정이 필요합니다.

Kirchhoff 법칙과 Lambert 법칙에 따르면, 방사 플럭스 ϕλ 는 방출 복사, 반사 복사, 투과 복사의 합으로 표현되며, θ는 표면 법선과 복사 방향 사이의 각도, φ는 반공간 내 방향각, cos(θ) 항은 Lambert 코사인 법칙을 반영합니다.

방사 플럭스 ϕλ 는 모든 적외선 방사원에 대해 적외선 센서의 대역폭에 걸쳐 Planck 법칙을 적분하고 Lambert 법칙을 고려하여 구할 수 있습니다. 여기서는 방사율이 범위 내에서 거의 일정하고, 센서 감도가 1이라고 가정하면 식은 다음과 같이 단순화됩니다. 변수 Tobj,Tp,Tτ ​는 각각 물체 온도, 반사 원 온도, 배경 온도를 나타냅니다.

따라서 검출기 신호 U는 모든 복사 플럭스의 조합입니다.

단순화하여 Stefan-Boltzmann 법칙에 따르면, 표면에서 방출되는 총 적외선 에너지는 방사율과 절대온도의 4제곱에 비례합니다(전체 스펙트럼 λ₁=0, λ₂=∞).

실제 적외선 온도계는 제한된 스펙트럼 범위에서 작동하므로, 이상적인 지수 n=4 대신 측정 파장과 스펙트럼 감도에 따른 유효 지수 n을 사용하며, 상수 c_i는 광학 파라미터를 대체하고 보정 계수로 작용합니다.

검출기 신호는 반사, 방출, 투과의 합이며, 센서 자체 방사를 차감한 값입니다.

역 방사 방정식을 풀어 센서는 측정된 적외선 신호를 물체 표면 온도에 대응하는 값으로 변환합니다.

이 식은 광학 경로에 창(window)이 없는 이상적인 측정 상황을 나타냅니다.

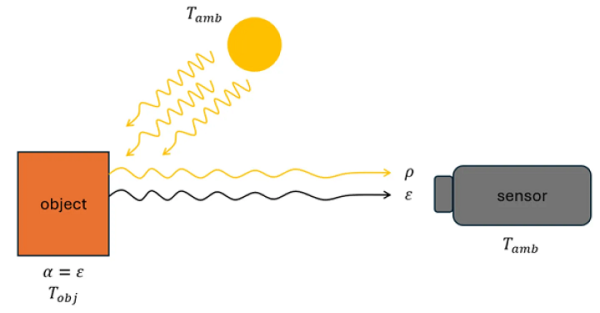
그림 2. 물체는 온도에 따라 적외선을 방출하며, 주변 복사의 일부를 반사합니다.

센서는 합성된 복사 플럭스를 감지하며, 물체의 실제 온도를 정확히 결정하기 위해 주변 반사와 내부 복사 보정이 필요합니다.

그림 2는 표준 측정 환경을 나타낸 예입니다. 투과가 무시되는 불투명 물체가 비접촉 열 센서에 직접 관측됩니다. 이 경우, 물체와 센서 사이에 투과 요소가 없으며, 물체는 높은 방사율과 광학적으로 두꺼워 투과율 τ=0으로 가정할 수 있습니다. Kirchhoff 법칙에 따라 ρ=1-ε이며, 센서와 주변 환경이 열평형에 있으므로 주변 온도 = 센서 온도(Tint=Tamb)로 가정합니다. 반사체 온도도 주변 온도(Tρ=Tamb)로 가정합니다. 따라서 식은 다음과 같이 단순화됩니다.

따라서 정확한 온도 측정을 위해서는 방사율에 대한 사전 지식이 필요하거나, 이를 보정하기 위한 현장(in-situ) 방법이 요구된다. 보정 계수 cintc​, cρ, cε 는 공장 보정(factory calibration) 과정에서 결정된다.

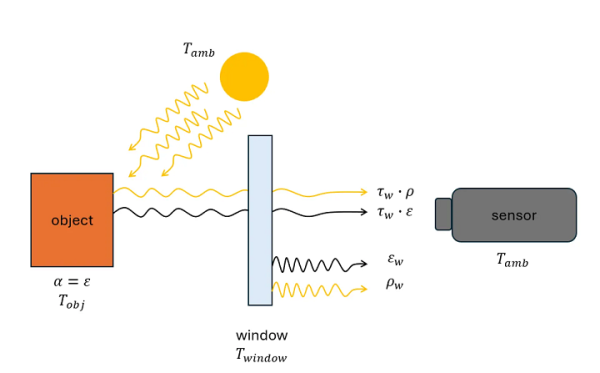
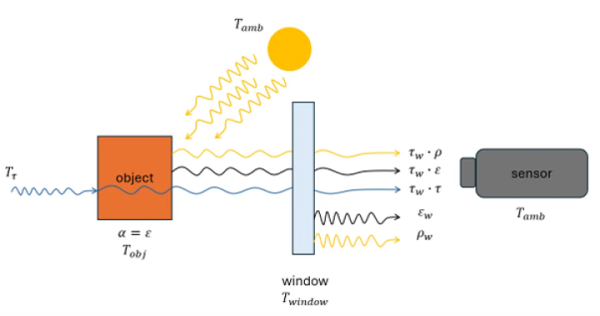
보다 복잡한 경우로는 그림 3에 나타난 것처럼, 물체와 센서 사이에 적외선 윈도우를 포함하는 상황이 있다. 물체는 자신의 온도에 대응하는 적외선 복사를 방출하는 동시에, 주변 환경으로부터의 일부 복사 에너지를 반사한다. 센서는 투과율이 τw 인 윈도우를 통과하는 전체 복사 플럭스를 측정한다. 이 윈도우는 입사하는 복사의 일부를 흡수하며, 또한 자신의 온도 Twindow 에 따라 추가적인 복사를 방출한다.

그림 3. 물체와 센서 사이에 적외선 창이 있는 경우 물체는 자신의 온도에 따라 적외선을 방출하며, 주변 복사의 일부를 반사합니다.

센서는 창을 통해 총 복사 플럭스를 측정합니다. 창은 투과율 τw를 가지고 일부 적외선을 흡수하며, 창 온도 Twindow에 따라 추가 복사를 방출합니다.

총 복사 플럭스는 다음과 같이 표현됩니다.

식 변형으로 물체 온도 계산:

요약

- 적외선(IR) 센서는 방출, 반사, 투과된 복사를 측정합니다.

- 물체 온도 계산에는 Planck 법칙과 Stefan-Boltzmann 법칙이 적용됩니다.

- 방사율(emissivity), 주변 반사, 센서 자체 방사(self-radiation)를 보정해야 합니다.

출처

- Hecht, Eugene. Optik, Berlin, Boston: De Gruyter, 2018. https://doi.org/10.1515/9783110526653

- Miller, J. L., Friedman, E., Sanders-Reed, J. N., Schwertz, K., & McComas, B. (2020). Photonics rules of thumb (No. PUBDB-2021-03249). Bellingham, Washington: SPIE Press. https://doi.org/10.1117/3.2553485

- De Witt, Nutter: Theory and Practice of Radiation Thermometry, 1988, John Wiley & Son, New York, https://doi.org/10.1002/9780470172575