기술 자료실

하나의 문제를 해결하고, 또 다른 문제를 만들어내는:Two-Color 파이로미터의 Ratio Method

장점, 가정, 그리고 한계

Ratio method는 서로 다른 두 파장에서 동작하는 두 개의 검출기로부터 측정된 신호를 이용하여, 하나의 온도와 하나의 방사율 비(emissivity ratio)를 동시에 만족시키는 값을 구하려는 방법이다. 이 방식은 two-color(또는 two-wavelength) 파이로미터에서 사용되며, 대상 물체의 실제 표면 온도를 추정하는 데 목적이 있다. Two-color 파이로미터는 서로 다른 파장에서 복사 에너지를 측정하는 두 개의 검출기를 사용한다.

Two-color 파이로미터의 기본 개념은 비교적 단순하다. 일반적인 비접촉 온도 측정에서는 두 개의 미지수가 존재하는데, 하나는 물체의 실제 온도이고 다른 하나는 방사율이다. 그러나 단일 검출기를 사용하는 경우 측정값은 하나뿐이므로, 이 문제는 본질적으로 해를 가질 수 없다. Two-color 방식은 서로 다른 파장에서 동작하는 두 번째 검출기를 추가함으로써 측정값을 하나 더 제공한다. 겉보기에는 두 개의 미지수(온도와 방사율)에 대해 두 개의 독립적인 측정값이 존재하므로 문제가 해결된 것처럼 보인다. 하지만 실제로는 미지수가 세 개이다. 방사율은 파장에 따라 달라질 수 있기 때문에, 한 파장에서의 방사율은 다른 파장에서의 방사율과 다를 수 있다. 따라서 실제 표면 온도를 계산하기 위해서는 여전히 방사율 비에 대한 가정이 필요하다.

광학 경로 또는 배경 영향 역시 ratio 파이로미터의 중요한 특징 중 하나이다. 예를 들어, 광학 경로에 먼지, 수증기, 또는 반투명 창이 존재한다고 가정해 보자. 이 경우 두 파장에서의 감쇠가 동일하다면, ratio 파이로미터는 이러한 손실을 상쇄할 수 있다. 실제로 균일하게 오염된 렌즈나 두 채널에 유사하게 영향을 미치는 연기와 같은 광대역 장애물은 ratio 측정을 통해 상당 부분 보정된다. 그러나 광학 경로의 투과율이 파장에 따라 다를 경우(non-grey attenuation), 이는 측정된 방사율 비를 변화시키는 효과를 가지며 방사율 변화와 동일한 방식으로 오차를 유발한다. 즉, 방사율 비가 일정하더라도 채널 간 투과율 차이는 방사율 오차와 유사한 측정 오차를 발생시킬 수 있다.

Two-color 파이로미터에서 일반적으로 사용되는 가정은 두 파장에서의 방사율이 거의 동일하다는 것이다. 즉 ε1(λT)=ε2(λB) = ε1​(λT​)=ε2​(λB​) 가 성립한다고 본다. 만약 ε1(λT) 가 ε1(λB) 와 같지 않다면, 보정이 필요하며 이를 일반적으로 “Slope” 또는 방사율 비(emissivity ratio)라고 한다.

기울기는 다음과 같이 정의된다:

εslope=(ε1(λT))/(ε2(λB))≈1

Ratio 파이로미터를 해석적으로 표현하는 한 가지 방법은 다음과 같다. 방사율은 동일한 온도에서 실제 물체의 복사 휘도를 흑체 복사 휘도로 나눈 값으로 정의된다. 여기에 플랑크 법칙을 대입하고 λ5 항과 복사 상수 c1​이 소거된다는 점을 고려하면, 다음과 같은 식을 얻을 수 있다.

εslope=(ε1(λT))/(ε2(λB))=(M(λT)(λT,TT))/(M(λT)∘(λT,T))∙(M(λB)∘(λB,T))/(M(λB)(λB,TB))=⋯=(e(c2/(λT∙TT)

두 파장에서의 방사율 비를 취함으로써, 두 파장에서의 등가 밝기 온도 TT, TB​와 실제 표면 온도 T 사이의 관계가 정의된다.

이 방정식은 해석적인 해를 갖지 않으므로, 실제 계산에서는 반복 계산을 통한 수치 해석이 필요하다. 이를 단순화하기 위해 ratio temperature가 도입된다. Ratio temperature는 두 파장에서 측정된 복사 신호의 비와 동일한 비를 가지는 흑체의 온도이다.

1/TR=Λ(1/(λTTT)−1/(λBTB))

비엔 근사(Wien’s approximation)와 방사율 관계를 이용하면 다음과 같은 간단한 식을 얻을 수 있다.

1/T=1/TR+Λ/c2ln(εslope)

비엔 법칙은 플랑크 법칙의 일부 항을 무시하기 때문에 저온 또는 장파장 영역에서는 오차를 유발할 수 있다. 그러나 two-color 파이로미터가 주로 사용되는 고온·단파장 영역에서는 일반적으로 충분히 정확한 결과를 제공한다.

여기서 Λ는 두 파장에 의해 정의되는 유효 파장으로, 실제 물리적 파장은 아니며 온도 계산식에 등장하는 수학적 개념이다.

Λ=(λBλT)/(λT−λB)

이 식에서 알 수 있듯이, 두 측정 파장이 서로 가까워질수록 유효 파장 Λ는 급격히 증가한다. 파장을 가깝게 선택하면 두 파장에서의 방사율 비가 보다 안정적이라는 장점이 있지만, 동시에 방사율 비의 작은 오차가 계산된 온도에 큰 영향을 미치게 된다. 이는 two-color 파이로미터에서 피할 수 없는 근본적인 트레이드오프이다.

검출기 신호에서 온도로: Ratio Method의 수학적 기반

Ratio 의존성을 표현하는 또 다른 방법은 다음과 같다. 두 파장에서의 측정 대역폭이 매우 좁아 단색광 조건(Δλ ≪ λ)을 만족하고, 두 파장이 서로 가깝고(λB≈λT), 방사율이 거의 동일하다고 가정하면 식은 단순화된다. 검출기는 수신된 적외선 플럭스에 비례하여 신호를 출력하므로, 플랑크 법칙을 이용해 다음과 같은 관계를 얻을 수 있다.

UT/UB (ϕ(λT)(λ1,Tobj))/(ϕ(λB)(λ2,Tobj))=(ε1(λT))/(ε2(λB))(M∘(λT,Tobj))/(M∘(λB,Tobj))=⋯=εslope(λ5B)/(λ5T)(e(c2/(λB∙T))−1)/(e(c2/(λT∙T))−1)≈εslope(λB/λT)5e(c2/(λT∙T)−c2/(λB∙T))=εslope(λB/λT)5e(c2/T(λB−λT)/(λBλT))=εslope(λB/λT)5e(−c2/TΛ)

이 식은 두 채널의 신호 비가 온도의 함수로 지수적으로 변화함을 보여준다.

그림 1은 전형적인 ratio 파이로미터(R1M)의 검출기 신호를 대상 온도의 함수로 나타낸 것이다. 두 개의 실선은 서로 다른 적외선 파장에서 동작하는 채널 1과 채널 2의 분광 신호 응답을 나타낸다. 플랑크 법칙에 따라, 각 single-color 채널의 신호는 온도가 증가함에 따라 지수적으로 증가하지만, 파장에 따라 크기와 기울기는 서로 다르다.

점선은 두 채널 신호의 로그 비(logarithmic ratio)를 나타낸다. 원 신호와 달리, 이 비율 응답은 넓은 온도 범위에서 거의 선형적인 특성을 보인다. 이러한 특성 덕분에 두 채널 간 방사율 비가 일정하다는 가정 하에, 방사율의 절대값을 정확히 알지 못하더라도 안정적인 온도 측정이 가능하다.

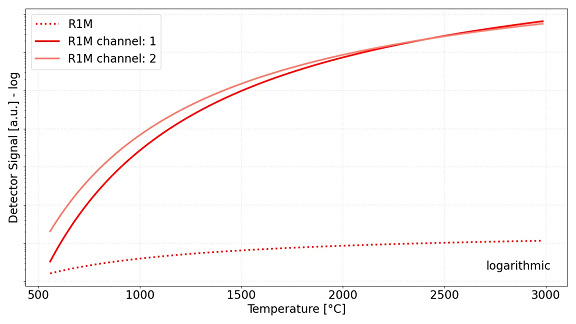
그림 1. 두 채널 ratio 파이로미터에서 대상 물체 온도에 따른 검출기 신호 응답.

실선은 각 채널의 복사 신호를 나타내며, 플랑크 법칙의 특성에 따라 온도가 증가함에 따라 지수적으로 증가한다.

점선은 두 채널 신호의 비율을 나타낸다. 개별 신호는 지수적으로 증가하지만, 신호 비는 전체 온도 범위에서 거의 선형적인 특성을 유지한다.

위의 식을 바탕으로 물체의 온도는 다음과 같이 정리할 수 있다. 여기서도 추가적인 단순화를 위해 Wien 근사가 적용된다.

T=c2/(Λ[ln〖(εslope)+ln((λ5B)/(λ5T))−ln(UT/UB)〗])

Emissivity Slope 오차가 Two-Color 온도 측정을 왜곡하는 방식

불행히도, ratio 파이로미터가 방사율 항을 상쇄할 수 있다는 장점에는 대가가 따른다. 온도 오차는 방사율 비(emissivity ratio)의 불확실성에 매우 강하게 의존한다. 두 파장이 서로 너무 가까우면 유효 파장 Λ가 매우 커지며, 그 결과 계산된 온도는 작은 오차에도 훨씬 민감해진다. 반면, 좁은 파장 범위에서는 방사율 slope가 더 안정적이거나 더 잘 알려져 있을 수 있어, 전체적인 정확도가 향상될 수도 있다.

방사율 비가 아주 조금만 변해도 온도 계산 결과에는 눈에 띄는 변화가 발생한다. 이 민감도는 ratio 식을 온도에 대해 풀고, 온도를 slope에 대해 미분한 뒤, 지수항과 로그항을 단순화하기 위해 Wien 근사를 적용하면 다음과 같이 표현할 수 있다.

ΔT/T≈(−ΛT)/c2Δεslope

방사율 비의 불확실성이 몇 퍼센트 수준에 불과하더라도, 고온 영역에서는 수십 도에 이르는 온도 오차를 유발할 수 있다. 실제 측정 환경에서는 사소해 보이는 방사율 비 변화가 계산된 온도를 크게 이동시키는 결과를 초래할 수 있다.

많은 상용 시스템들은 두 개의 서로 다른 파장에서 동작하는 검출기를 사용하고, “ratio” 모드를 통해 방사율 영향을 보정함으로써 “진정한(True)” 온도를 측정한다고 홍보한다. 그러나 정확한 온도 측정은 두 파장에서의 방사율 비가 알려져 있거나, 최소한 측정 중에 안정적으로 유지된다는 전제에 의존한다. 이 방식의 대가는 명확하다. 방사율 비의 변화에 극도로 민감하다는 점이다. 어떤 경우에는 두 검출기 신호 간의 1 °C 차이가 two-color 온도 결과를 최대 10 °C까지 이동시킬 수 있다. 일반적으로 ratio 파이로미터는 방사율 비가 측정 중 일정하게 유지될 때에만 진정한 의미에서 방사율 독립적이라고 할 수 있다.

그림 2는 two-color 파이로미터에서 방사율 slope 변화가 온도 측정 정확도에 미치는 영향을 보여준다. Ratio 파이로미터는 일정한 방사율에 대해서는 보정 효과를 가지지만, 파장별로 방사율 변화가 다르게 발생하면 slope가 변하게 되고, 이로 인해 측정 오차가 발생한다.

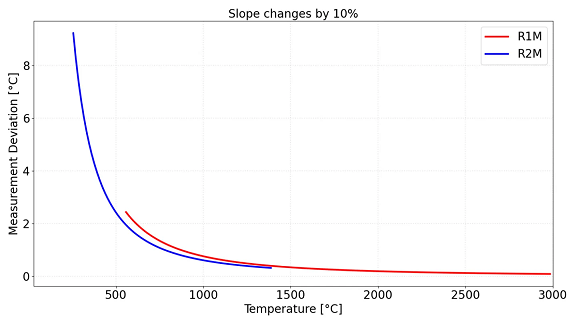
그림2. Two-color 파이로미터에서 방사율 slope 변화가 온도 측정 정확도에 미치는 영향.

곡선은 채널 간 방사율 비가 ±10% 변했을 때 발생하는 온도 측정 편차를 나타낸다.

복사 신호가 커지는 고온 영역에서는 slope 변화에 대한 민감도가 감소하므로 오차 크기가 줄어든다.

왜 Ratio 파이로미터가 Single-Color 장비보다 더 큰 오차를 보일 수 있는가

Slope 변화 외에도, 각 채널의 시스템 정확도를 반드시 고려해야 한다. Ratio 온도는 개별 채널의 온도 측정값을 기반으로 계산되기 때문이다. 이를 평가하기 위해, single-color 채널의 온도 측정값에 편차가 존재한다고 가정하고 ratio 온도 방정식을 계산한다. Single-color 측정 불확실성이 ratio 파이로미터의 거의 선형적인 방사율 비 민감도 방정식을 통해 전달되기 때문에, ratio 온도는 동일한 장비를 single-color 모드로 사용할 때보다 더 큰 편차를 보일 수 있다.

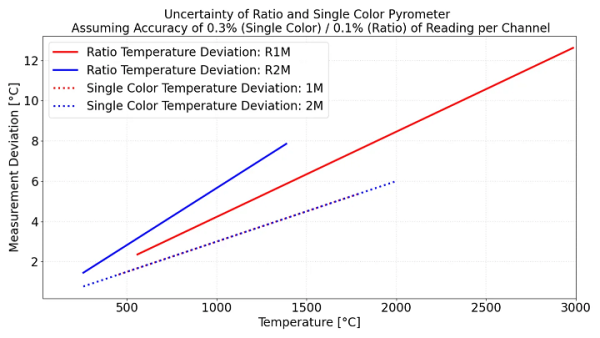
그림 3은 이상적인 흑체 보정원을 기준으로 시스템 정확도를 비교한 결과를 보여준다. Single-color 파이로미터는 판독값 기준 0.3%의 정확도를, ratio 파이로미터는 채널당 0.1%의 보정 정확도를 가정하였다. 실제 대상 온도가 1000 °C일 때, Channel 1이 999 °C, Channel 2가 1000.0 °C를 읽는 경우—모두 일반적인 단일 채널 보정 오차 범위 내임에도 불구하고—ratio 온도는 최대 약 4 °C의 편차를 보일 수 있다.

Two-color 파이로미터는 작은 채널 간 불일치나 방사율 비 가정의 작은 오차를 증폭시킬 수 있다. 이는 유효 파장 개념에서 직접적으로 기인한다. 서로 매우 가까운 파장을 선택하면 방사율 비를 1로 가정하기 쉬워지지만, 동시에 유효 파장이 증가하여 온도가 slope 변화와 채널 간 차이에 더욱 민감해진다.

경험적인 기준으로 보면, 두 채널 간 약 1 °C의 차이는 ratio 결과를 최대 약 10 °C까지 이동시킬 수 있다.

그림 3. 대상 온도에 따른 ratio-color 파이로미터(실선)와 single-color 파이로미터(점선)의 측정 편차 비교.

계산에는 single-color 정확도 0.3%, ratio 모드는 채널당 0.1% 정확도를 가정하였다.

Ratio 곡선의 더 큰 기울기는, 특히 유효 파장이 클수록 작은 채널 오차에 대해 온도가 훨씬 민감해짐을 보여준다.

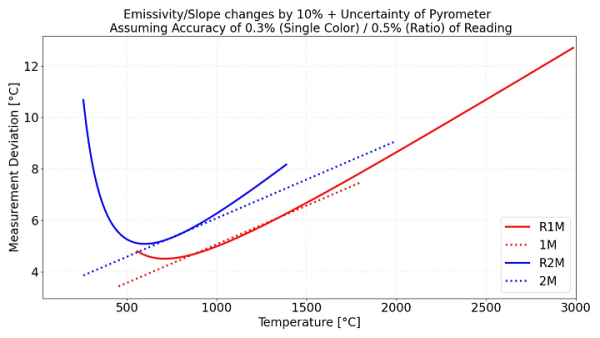
그림 4는 시스템 정확도와 slope 변화의 영향을 함께 고려한 결과를 나타낸다. 흥미롭게도, 단파장 single-color 파이로미터는 경우에 따라 dual-color 파이로미터와 유사한 성능을 보일 수 있다.

그림 4. 방사율 10% 변화(single-color, 점선) 또는 방사율 비/slope 10% 변화(two-color, 실선)가 지시 온도에 미치는 영향.

기기 정확도는 single-color 0.3%, ratio 모드는 전체적으로 0.5%를 가정하였다.

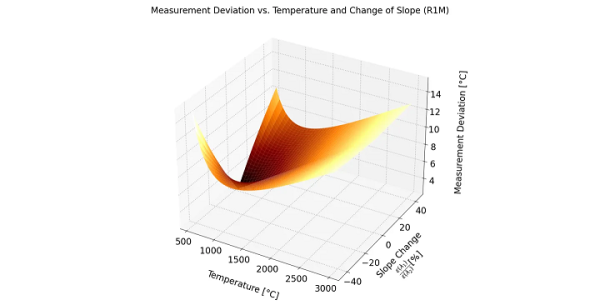
그림 5는 ratio 파이로미터에서 방사율 비 가정과 시스템 정확도가 온도 측정에 미치는 영향을 3차원적으로 나타낸 것이다. x축은 대상 온도, y축은 방사율 비의 상대 변화(±40%), z축은 측정된 온도 오차를 나타낸다. 비교적 작은 slope 불일치도, 특히 저온 영역에서는 매우 큰 온도 편차를 유발할 수 있음을 보여준다. 이는 ratio 파이로미터가 방사율 slope 오차에 매우 민감하다는 점을 강조하며, 특히 저온 영역에서의 적용 시 스펙트럼 방사율 특성에 대한 충분한 이해가 필요함을 시사한다.

그림 5. R1M ratio 파이로미터에서 대상 온도와 방사율 slope 변화에 따른 온도 측정 오차.

저온 영역과 큰 스펙트럼 방사율 불일치 조건에서 오차가 급격히 증가한다.

Two-Color 파이로미터가 효과적인 경우와 그렇지 않은 경우

전반적으로 ratio 파이로미터는 방사율 비가 안정적이고 신뢰할 수 있는 경우가 아니라면, single-color 파이로미터보다 반드시 더 정확하다고 할 수는 없다. 이는 two-color 장비가 자동으로 방사율 독립적이라는 흔한 오해를 바로잡아준다. 표면 상태 변화, 파장 의존적인 방사율 특성, 관측 각도 변화 등으로 인해 방사율 비 가정이 틀어질 경우, 측정 오차는 매우 커질 수 있다.

그럼에도 불구하고 ratio 파이로미터는 가혹하거나 변화가 많은 환경에서 중요한 장점을 제공한다. 오염된 광학계, 관측 창, 부분적으로 가려진 대상 등으로 인해 발생하는 균일한 신호 손실을 효과적으로 보정할 수 있다. 또한 대상 크기 변화나 정렬 오차에 덜 민감하므로, 이동 중이거나 부분적으로 가려진 물체의 온도 측정에 특히 유리하다. 방사율 비가 알려져 있거나 합리적으로 안정적인 조건에서는, ratio 파이로미터는 conventional single-color 방식으로는 어려운 응용 분야에서도 신뢰성 있는 비접촉 온도 측정을 가능하게 한다.

요약

- Two-color 방식은 본질적으로 “더 정확한” 방법이 아니다. 이는 특정 조건에서만 강인한 방식으로, 두 파장에서의 방사율 비가 일정하게 유지되고 광학 경로 감쇠가 두 채널에 동일하게 작용하는 경우에 가장 효과적이다.

- Ratio 파이로미터는 서로 다른 두 파장에서 동작하는 두 개의 검출기를 사용하여 온도와 방사율을 동시에 추정하려는 방식이다. 반면 single-color 파이로미터는 정확한 온도 측정을 위해 방사율 값이 사전에 알려져 있어야 한다.

- 완전히 방사율 독립적인 방식은 아니다. Two-color 방식은 두 파장에서의 방사율이 서로 유사하거나 예측 가능하다는 가정에 의존한다. 이 방사율 비(또는 “slope”)가 변하면, 계산된 온도는 크게 왜곡될 수 있다.

- Slope 오차에 매우 민감하다. 파장 간 방사율 비의 작은 변화만으로도 큰 온도 오차가 발생할 수 있으며, 특히 저온 영역에서 그 영향이 더욱 두드러진다.

- 가혹한 환경에서는 강점을 가진다. 먼지, 연기, 오염된 광학계와 같은 조건에서는 두 파장이 동일하게 영향을 받는 경우에 한해, ratio 파이로미터가 single-color 파이로미터보다 더 안정적인 성능을 보인다.

- Slope가 안정적인 경우에 가장 효과적이다. 방사율 비가 일정하게 유지되는 조건에서는 ratio 파이로미터가 매우 유용하며, 부분적으로 가려진 시야에서도 신뢰성 있는 측정이 가능하다.

- 방사율이 잘 알려져 있고 시야 조건이 깨끗한 경우에는, single-color 파이로미터가 two-color 방식보다 절대 정확도 측면에서 더 우수할 수 있다.

출처

- Hecht, Eugene, Optik, Berlin, Boston: De Gruyter, 2018. https://doi.org/10.1515/9783110526653

- Miller, J. L., Friedman, E., Sanders-Reed, J. N., Schwertz, K., & McComas, B. (2020). Photonics Rules of Thumb (No. PUBDB-2021-03249). Bellingham, Washington: SPIE Press. https://doi.org/10.1117/3.2553485

- De Witt, D. P., & Nutter, G. D., Theory and Practice of Radiation Thermometry, 1988, John Wiley & Sons, New York. https://doi.org/10.1002/9780470172575

- Risch, Timothy K., User’s Manual: Routines for Radiative Heat Transfer and Thermometry, NASA/TM—2016–219103, July 2016.

- Advanced Energy Industries, Inc., Understanding Two-Color (Ratio) Pyrometer Accuracy, Advanced Energy Industries, Inc.